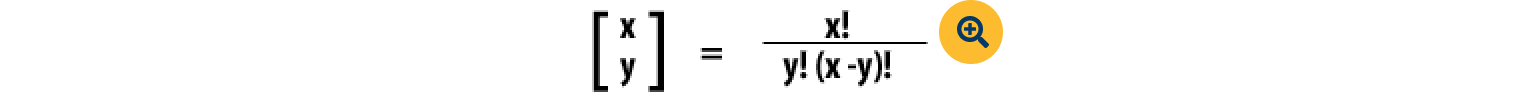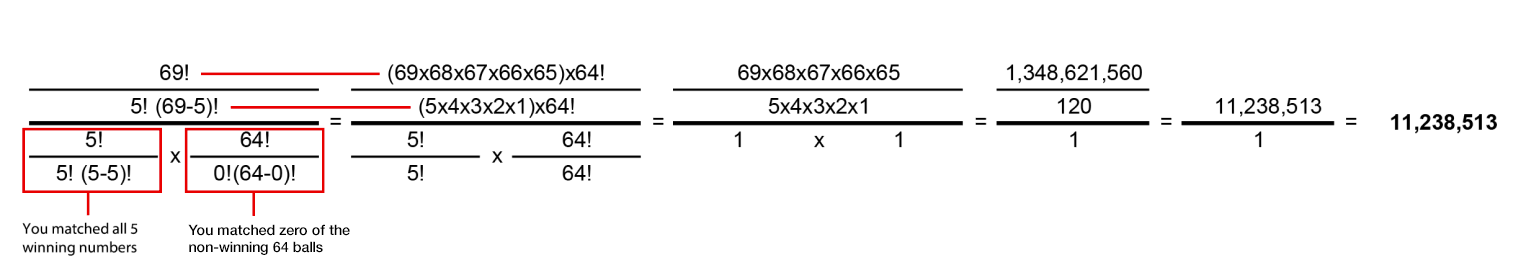Powerball is a multi-state game that gives players nine ways to win cash prizes. In addition to the jackpot, the game offers second-level prizes of $1 million and third-level prizes of $50,000.
Jackpots start at $20 million and increase by a minimum of $2 million based on current game sales and interest rates.
The game is operated by the Multi-State Lottery Association (MUSL) in Des Moines, Iowa.
Next Drawing: Wednesday, Jul 9
Understanding Powerball Chances
No matter how many people play Powerball, the chances of winning never change. The chances of winning are based on the amount of number combinations, not the number of players. Quick Pick tickets are generated randomly by the terminal at the retailer, and there is no central computer that is controlling ticket generation.
Many people ask us to explain how their chances of winning are determined. So, let's start at the beginning!
The Powerball game is played by selecting five numbers out of 69 choices (the numbers from 1 to 69), and by selecting one extra number from 1 to 26 (that's the Powerball). When it's time to draw the winning numbers, there are two machines tumbling the ball sets at the same time: one machine has the 69 white balls, and the other one has the 26 red "Powerballs." So the Powerball game is like holding two drawings at the same time; two independent events played simultaneously. Any chances of winning has to consider what happens to the number selections within one drum combined with the possibilities of what's happening in the other drum. That idea is really important to keep in mind. A winning set of numbers will be whatever five balls are selected out of the white-ball drum plus the one ball selected from the red-ball drum.
But the chances of winning look confusing because even at the smallest winning level (just getting the Powerball right), many people think the chances of winning that should be 1 in 26 (one correct choice out of a drum of 26 balls, right?). But we're not just playing that one drum; in order to say you "only matched the Powerball" that means you have to have missed all five of the white balls that were chosen in that other drum! The chances of doing that combined with your 1-in-26 shot of getting the Powerball actually come out to being 1 in 38.3. In other words, there is one chance in 38.3 that you'd pick the winning Powerball number and miss selecting any of the five winning white-ball numbers.
So when you hear a "chances of winning" calculation, it's describing the chance that you will have chosen the winning numbers, including the chances you chose numbers that didn't get drawn. Since there are several ways to win (from zero to all five of the white balls, with and without having the Powerball), that means people who calculate the chances of winning have to figure each level of winning or not winning in each of the two drums.
For example, in order to win the big jackpot, a winner must have chosen all five white balls correctly, as well as the Powerball number. To describe the chances of winning, you have to say what your possible chances are of choosing the winning balls against choosing any of the 64 non-winning balls in the one drum, combined with your chances of choosing the winning Powerball against choosing any of the 25 non-winning red balls in that drum. That's a lot of combinations - more than 292 million, in fact. But there's an easy formula that gets you there.
Where Do You Start?
Any calculation of chances for a Lottery game involves three basic elements:
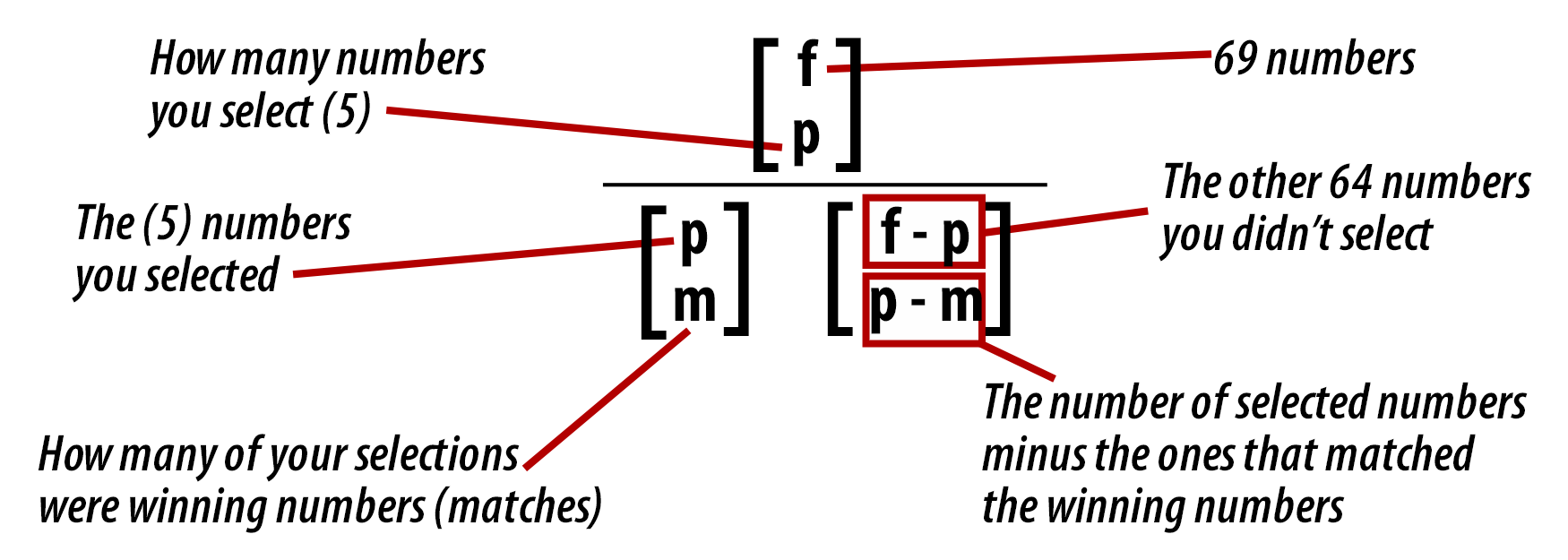
- The total number of balls (numbers) you are choosing from, which is called the field or (f).
- The number of balls the player selects on his\her play slip, which is called the pick or (p).
- The number of correct matches between the player's picks and the numbers drawn out of the machine, which is called the match (m).
The mathematical formula looks like this:
Each part of that formula, which is in parentheses, is a "binomial coefficient," which is a calculation on how many ways there are to make different combinations. In our case, we're talking about how many combinations of lottery balls you could make with a set of 69 (or 26) balls. What that means is that for whatever numbers you have, the binomial can be rewritten as follows:
X! means "x factorial"; for example, 5! is 5 x 4 x 3 x 2 x 1 = 120.
Powerball Chances of Winning the Jackpot:
(5 of 5 plus the Powerball)
Now we're ready to look at winning that jackpot!
To do that, we said you'd have to describe the chances of picking five numbers including 64 non-winning ones out of a total of 69. Then you combine that with the figure to describe your chances of picking one winning Powerball number, including choosing 25 non-winning numbers. So using our binomials and factorials, it looks like this:
So, 69 x 68 x 67 x 66 x 65 = 1,348,621,560 and 5 x 4 x 3 x 2 x 1 = 120; divide one by the other:
1,348,621,560 / 120 = 11,238,513 (chances of 11,238,513 to 1 of picking all 5 white balls out of 69)
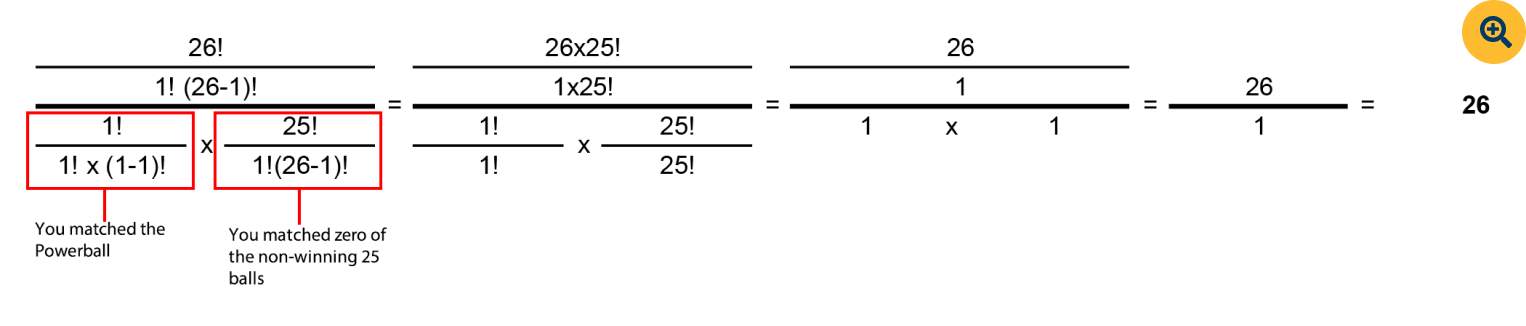
And don't forget that now we have to combine the possibilities of choosing the Powerball, which we know is one in 26. That formula works just like the one above:
So, 11,238,513 / 1 x 26 / 1 = 292,201,338.
Now, that's just one win scenario: the big jackpot. But you can also win eight other prizes ranging from $4 to $1,000,000.
(In order to win a prize, your Powerball number must at least match the Powerball number drawn, or you must match at least three of the five white-ball numbers drawn.)
When you combine the chances of all those levels and all those combinations, it comes out to 1 in 24.87.
So each player has a 1-in-24.87 chance to win any of the prizes (jackpot, $1,000,000, $50,000, $100, $7, or $4)!
We hope this helps to better explain the chances of winning the Powerball jackpot.